مباراة توظيف الأطر النظامية للأكاديميات - دورة دجنبر 2021
اختبار في ديداكتيك المواد المدرسة بالتعليم الابتدائي (اللغة العربية، الفرنسية، الرياضيات والعلوم)
قبل الشروع في معالجة درس الحركة، قدمت مدرسة لمتعلمات ومتعلمي المستوى الخامس ابتدائي التعليمة الآتية: "أنجز(ي) رسما تخطيطيا للعظام داخل الذراع وفسر(ي) ما يحدث عند ثني الطرف." تقدم الوثيقة أسفله عينة من إجابات المتعلمات والمتعلمين:
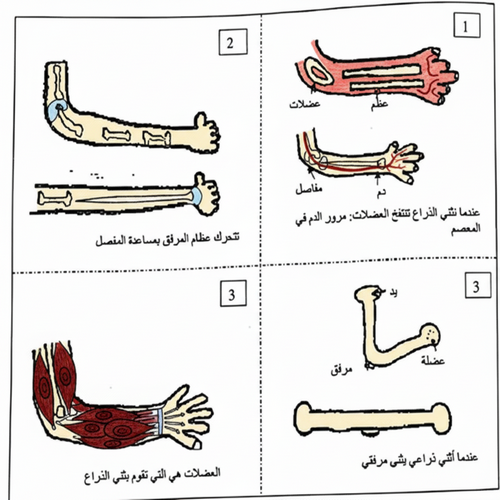
النموذج 2: التركيز على العظام والمفاصل دون ذكر العضلات.
النموذج 4: إدراك دور العضلات في ثني الذراع.

الجزء الأول:
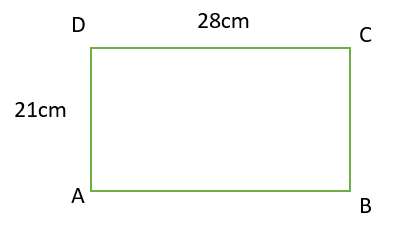
التلميذ أحمد: "لماذا 100cm؟"
التلميذة آمال: "إذا أخذنا 3 من 28 وأضفناها إلى 22، نحصل على شكل مكون من أربعة أضلاع قياس كل ضلع منها يساوي 25cm وله نفس المحيط."
1) إذا أخذت مكان الأستاذ كيف سيكون جوابك على سؤال التلميذ أحمد؟"نص القانون الإطار 51.17 في المادة 3 على أن المنظومة تسعى إلى:
إكساب المتعلم المهارات والكفايات اللازمة، التي تمكنه من الانفتاح والاندماج في الحياة العملية، والمشاركة الفاعلة في الأوراش التنموية للبلاد؛
تشجيع التحفيز على قيم النبوغ والتميز والابتكار، وتنمية القدرات الذاتية للمتعلمين، وتطوير الحس النقدي لديهم، وحفز الذكاء وإتاحة الفرص أمامهم للإبداع والابتكار، وتمكينهم من الانخراط في مجتمع المعرفة والتواصل."